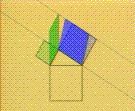
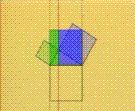
Ce texte veut fournir des éléments de réflexion sur le plan pédagogique, historique et épistémologique aux enseignants de mathématiques. Le but est d'éclaircir le lien entre vidéos et travail en classe. Il est à compléter par deux articles principaux qui figurent sur ce site :
- L'article dans la rubrique "techniques" sur les Techniques de visualisation employées dans la vidéo "Le théorème de Pythagore" écrit par Tom Apostol qui se trouve .
- L'article sur l'Histoire du théorème de Pythagore dans la rubrique article, ainsi que d'autres articles sur les mathématiques babyloniennes, grecques et arabes et sur la théorie des proportions.
Les vidéos nécessitent un travail écrit des élèves pour capitaliser ce qu'ils ont compris, le rédiger et le traduire en démonstration. Pour aider le travail de préparation des enseignants, des captures d'écran et des documents "bruts" à adapter par les enseignants seront fournis pour chaque animation. L'enseignant pourra utiliser de tels documents, le compléter par les consignes de travail qu'il souhaite donner à ses élèves. Ces fiches de travail seront complétées par des références à d'autres sites pédagogiques, en particulier des sites contenant des animations utilisables en salle informatique.
Cette vidéo ne suit pas l'ordre d'introduction des notions dans les classes de collège. Les nombres sont connus comme prérequis et les notions de longueurs, d'aires et de volumes sont utilisées librement. Les triangles isométriques et les triangles semblables sont supposés connus, c'est à dire les notions de triangles de même taille et même forme et de triangles de même forme et de taille différente. Toutefois cette vidéo est utilisable en classe de quatrième en s'appuyant simplement, non sur les triangles semblables mais sur une notion d'agrandissement réduction. On utilise pour certaines démonstrations l'effet d'un agrandissement réduction de rapport r sur les longueurs, les aires et les volumes.
La vidéo ne suit pas non plus l'ordre d'exposition des Eléments d'Euclide, ni l'ordre du développement de l'histoire. Dans les Eléments d'Euclide, la proposition appelée aujourd'hui Théorème de Pythagore apparaît à la fin du premier livre. Les seuls nombres utilisés sont les entiers. La théorie des proportions est établie dans le livre 5 et appliquée dans le livre 6. L'équivalence établie dans la vidéo entre la proposition 31 du livre 6 d'Euclide et la proposition 47 du livre 1 suppose comme prérequis les triangles semblables. Ce point sera étudié en détail.
Dans l'histoire la signification même de l'énoncé du théorème de Pythagore a changé et ceci est bien illustré par une séquence de la vidéo intitulée "Interprétation géométrique du théorème de Pythagore".
-
Chez Euclide, l'énoncé signifie que le carré géométrique construit sur l'hypoténuse d'un triangle rectangle peut être décomposé en deux rectangles dont on montre qu'ils sont égaux au carrés géométriques construits sur les deux côtés de l'angle droit. L'égalité se démontre par des méthodes géométriques combinant déplacaments, égalités de triangles et déformations que nous désignons par coulissement.
-
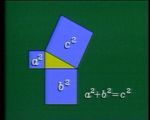A notre époque l'interprétation de l'énoncé est une égalité numérique où on mesure l'hypoténuse, on élève le nombre obtenu au carré, on fait de même pour les côtés de l'angle droit et on vérifie l'égalité entre nombres.
Le théorème de Pythagore apparaît comme réponse à deux problématiques différentes que l'on retrouve tout au long de l'histoire:
- Calcul d'un côté d'une triangle rectangle quand les deux autres sont connus. C'est dans cette problématique que se situent les différentes démonstrations faites dans la vidéo.
- Comment avec deux carrés en faire un seul. On trouve cette problématique dans certaines démonstrations indiennes, chinoises ou chez Clairaut. Voir l'article sur l'histoire du théorème de Pythagore dans ce site.
Les démonstrations du théorème de Pythagore reposent sur trois méthodes principales :
-
La méthode des aires où les raisonnements sont basés sur des invariances d'aires, justifiées par la méthode euclidienne, ou à l'aide de formules.
- L'usage de la similitude, c'est à dire de triangles de même forme.
-
Des méthodes de puzzles ou de découpages, assez visuels, quelquefois considérés comme évidents et peu justifiés par un discours mathématiques d'accompagnement.
On pourra consulter sur ce point le livre "Les curiosités géométriques" de Fourrey et l'article "Le théorème de Pythagore" déjà cité où de nombreuses démonstrations sont visualisées à l'aide d'applets.
On analysera les différents type de démonstrations à l'oeuvre dans la vidéo. Elles utilisent un langage visuel et le mouvement. Toute cette bande suppose comme prérequis la notion de triangles de même forme (triangles semblables). Les différentes animations présentent selon le cas :
- des démonstrations presque complètes au niveau mathématique, qu'il suffit de traduire dans le langage écrit;
- des démonstrations qui nécessitent l'explicitation d'un point difficile, évident visuellement;
- de simples monstrations comme une très jolie monstration par découpage que l'on peut adapter en une vraie démonstration au prix d'un travail important et parfois un changement de point de vue.
On retrouve à propos des animations informatiques le débat sur le rôle des démonstrations "pour convaincre" ou "pour éclairer" dont on parle en histoire des mathématiques. Voici donc avec ces preuves animées de nouvelles démonstrations, utilisant un autre langage, visuel celui-là que le langage écrit des mathématiques. On constatera que les animations fournissent des démonstrations très puissantes et l'on doit réfléchir aux spécificités de ce langage visuel. Lorsque le professeur voudra faire rédiger par écrit une démonstration illustrée par une animation vidéo, il sera amené à expliciter ce changement de code et à faire nommer les point des objets géométriques. Si on veut obtenir des élèves, ce qui est indispensable, un travail écrit suite à l'utilisation par exemple d'une animation pour montrer une propriété il faut explicitement revenir à l'usage de nommer les points pour expliciter les différentes étapes de la démonstration.
Toutes les vidéos ont une forte composante historique pour replacer les mathématiques dans l'histoire et dans les différentes civilisations. La vidéo montre des extraits de documents originaux dans différentes civilisations. Elle montre que ce résultat est un des résultats fondamentaux des mathématiques. On n'y trouvera pas une analyse historique complète. Certaines démonstrations célèbres dans l'histoire sont choisies et présentées sous forme d'animations. On renvoie à l'article précité pour une présentation plus détaillée de ces démonstrations. Les vidéos peuvent aussi aider les enseignants à introduire l'histoire des mathématiques dans leurs classes et donner des thèmes pour des travaux personnels.
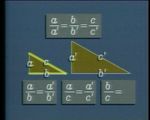
Les prérequis portent sur les propriétés des triangles de même forme ou triangles semblables. La bande vidéo sur "Similitude" présente toutes les propriétés utiles. Toutefois, si on utilise d'abord la bande sur le Théorème de Pythagore, les propriétés utilisées y sont présentées en préambule. Cela laisse une plus grande liberté au niveau pédagogique.
On va utiliser trois propriétés.
- Dans des triangles semblables, les côtés correspondants sont dans le même rapport.
- Dans une similitude, si les longueurs sont multipliées par r, les aires sont multipliées par son carré.
-
On utilise une déformation qui conserve les aires. Deux triangles de même base dont les sommets sont sur une même parallèle à la base ont les mêmes aires. De même si on déforme un parallélogramme en conservant un côté et en déformant le côté opposé parallèlement à ce côté, l'aire ne change pas. Cette déformation est une propriété essentielle pour les démonstrations dans les Eléments d'Euclide. Aujourd'hui il est facile de la justifier par un simple calcul d'aire. Dans les Eléments d'Euclide, elle est établie par des considérations géométriques simples. Voir l'article sur l'histoire du Théorème de Pythagore
Cette transformation est très facile à comprendre et à visualiser à l'aide d'animations. Plusieurs démonstrations utilisent cette transformation dans la vidéo. Elle est soulignée par un bruitage.
L'objectif de cette séquence est
de montrer l'utilité dans la vie des notions mathématiques. Les trois exemples sont introduits par une séquence filmée reprise ensuite par une animation. La première met en évidence que la droite est le plus court chemin d'un point à un autre. Ces exemples seront repris dans une séquence ultérieure intitulée "appliquer le théorème de Pythagore" quand on disposera du théorème et seront résolus alors.
Cette démonstration est très classique. On suppose que Pythagore a utilisé une justification de ce type avec des rapports de côtés en nombres entiers. On fait apparaître à l'aide de la hauteur sur l'hypoténuse deux triangles rectangles semblables entre eux et semblables au triangle initial. On écrit les rapports et on fait une peu d'algèbre. La nécessité d'équilibrer les équations en multipliant les deux membres par un même nombre est illustrée de façon convaincante.
La tablette babylonienne Plimpton 322 montre que ces triplets étaient connus 1200 ans avant Pythagore. On trouvera une étude de cette tablette dans l'article sur les mathématiques babyloniennes de ce site. Les triplets qui y figurent montrent que les babyloniens connaissaient une formule générale pour déterminer les triplets d'entiers côtés d'un triangle rectangle.
Voir les mathématiques babyloniennes et Babylonian_Pythagoras
Pythagore savait trouver deux séries de cas particuliers de triplets, en utilisant probablement des représentations figurées de nombres carrés. Voir l'article sur les mathématiques grecques sur ce site. On peut faire une séance sur les nombres figurés des pythagoriciens, qu'on peut intituler "des mathématiques avec des cailloux", où on retrouve certaines propriétés arithmétiques.
Les triplets pythagoriciens sont donnés par une formule générale. Si on multiplie les trois éléments d'un triplet par un entier, on obtient un autre triplet pythagoricien. Les triplets constitués par des entiers premiers entre eux sont donnés pour u et v entiers de parités différentes par u2 + v2, u2 - v2, 2uv. Voir le document sur les triplets.
Une proposition de document à donner à travailler aux élèves, avec la consigne : On considère un triangle ABC rectangle en B et on construit les carrés ABDE, BCFG et ACIJ. On trace la hauteur BH qui coupe IJ en K. Ecrire une légende pour chaque photo, en complétant le nom des points.
| 1 | 2 | 3 | 4 |
| 5 | 6 | 7 | 8 |
| 9 | 10 | 11 | 12 |
| 13 | 14 | 15 | 16 |
| 17 | 18 | 19 | 20 |
Cette démonstration comporte un point délicat. Bien que cela semble évident visuellement , il y a à justifier que trois droites sont concourantes: la hauteur et les deux droites parallèles aux côtés du triangle rectangle. Ici, on fait coulisser des parallélogrammes.
| a | b | c | d |
| e | f | g | h |
Voir les puzzles à la fin de l'article sur le théorème de Pythagore. On trouvera une variante du découpage de la vidéo.
La proposition 31 du livre VI dit que si on remplace les carrés construits sur les côtés d'un triangle rectangle dans la démonstration du la proposition 47 du livre 1 (théorème de Pythagore) par des figures semblables, la plus grande est "égale" à la somme des deux figures construites sur les côtés de l'angle droit.
Euclide a auparavant dans le livre 5 développé la théorie des proportions et l'applique dans le livre 6 à la gométrie plane. Les cas de similitude ont été établis avant la proposition 31. La vidéo établit une équivalence entre les deux propriétés mais elle a supposé comme prérequis les propriétés des triangles semblables et l'effet des similitude sur les longueurs, les aires et les volumes.
Sur le plan épistémologique, les deux propositions ne sont pas équivalentes dans la construction d'Euclide. Sur le plan historique de l'analyse des Eléments d'Euclide, le sens des mots rapports, égalité, surface etc … n'est pas le même que le notre. Un rapport n'est pas un nombre chez Euclide, et il n'est d'ailleurs pas défini autrement que par le fait qu'il a trait à la quantité. Seules sont définies des égalités et des comparaison de rapports à l'aide de le théorie du livre 5, appliquée ensuite à la géométrie dans le livre 6. De même, la lecture moderne du théorème de Pythagore porte sur des carrés de longueurs, c'est à dire des nombres tandis que chez Euclide le théorème de Pythagore porte effectivement sur des carrés, objets géométriques, où l'on peut partager le carré construit sur l'hypoténuse en deux rectangles égaux (mot employé par Euclide) respectivement aux carrés construits sur les deux autres côtés.
Sur le plan de l'enseignement, toute construction des nombres est escamotée et souvent le problème n'est même pas posé. On n'a donc pas affaire à une organisation déductive rigoureuse mais à des ilots déductifs sans construction d'ensemble. Il n'est pas bien entendu non plus question d'une théorie des proportions à la Euclide. Le point crucial escamoté est bien la relation numérique et géométrique et la construction en parallèle des nombres et de la géométrie. A partir d'un certain moment les nombres réels sont posés, existent et on les utilise en géométrie. Les problèmes épistémologiques posés par la vidéo existent à travers tout l'enseignement.
Pour résumer;
Si on sait associer un nombre à un rapport de longueur, d'aires ou de volumes, et si on part des propriétés connues des figures de même forme, alors effectivement, il y a cette équivalence. Le fond du problème est bien au niveau épistémologique la question des rapports et de leur définition comme nombre, ce qu'ils ne sont pas chez Euclide.
