LES IRRATIONNELS

28 décembre 2010 2 28 /12 /décembre /2010 15:15

Origine chez les pythagoriciens
Platon et le Thééthète
La démonstration par le pair et l'impair
Justification actuelle
La méthode d'antiphérèse
Calcul de racines carrées
Calcul par les fractions continues
Approximations décimales
Décimaux et calcul de racines carrées
Bibliographie

Origine chez les pythagoriciens

La question de l'irrationalité s'est posée chez les grecs sous la forme de la découverte de l'incommensurabilité de segments.

Les irrationnels

On ne dispose d'aucune trace précise de la découverte de l'incommensurabilité de lignes. On a seulement des témoignages de commentateurs Pappus, Proclus et Iamblicus qui écrivent plus de 7 siècles après les faits. Pappus la situe dans la secte pythagoricienne à propos de la diagonale du carré et l'attribue à Hyppasius, Proclus l'attribue à Pythagore. Iamblicus situe cette découverte des irrationnelles non pas pour la diagonale du carré, mais pour le partage d'un segment en extrême et moyenne raison, c'est à dire à propos du nombre d'or. Les textes du Platon et d'Aristote plus proches des pythagoriciens la situent dans la secte pythagoricienne et parlent de la diagonale du carré. Aristote dit que si la diagonale était commensurable avec le côté, alors un même nombre serait pair et impair. C'est la démonstration que nous connaissons bien. On pense généralement qu'il s'agit là de la première démonstration d'incommensurabilité de deux segments. Toutefois certains historiens émettent l'hypothèse que cette découverte ait été faite à propos du pentagone régulier étoilé qui était l'un des symboles de la secte pythagoricienne.

Démonstration par le pair et l'impair

On suppose que le rapport de la diagonale au côté est un quotient de deux entiers m et n. On peut remarquer qu'il n'y a pas besoin de supposer les entiers m et n premiers entre eux, mais seulement qu'ils ne sont pas tous les deux pairs. Ce qui n'utilise que des connaissances arithmétiques des pythagoriciens. On doit faire deux démonstrations.
a) Démontrer que le carré d'un nombre pair est pair et le carré d'un nombre impair est impair.
b) Supposons deux entiers non tous les deux pairs, tels que p² = 2 q². Montrer que p et q sont pairs. Conclure à une impossibilité.

Platon et le Thééthète

Le "Thééthète" a donné lieu à beaucoup de spéculations. Dans ce texte, Platon présente un mathématicien, Thééthète, qui vient de mourir, au moment où, dans sa jeunesse, il était élève du mathématicien Théodore et alors que Socrates avait rendu visite à son maître.

Thééthète: "Théodore que voici nous avait tracé quelques figures à propos des racines et nous avait montré que celles de trois pieds et de cinq pieds ne sont point pour la longueur commensurables avec celles de un pied, et les prenant ainsi, l'une après l'autre, il était allé jusqu'à celle de dix sept pieds et il s'était, je ne sais pourquoi, arrêté là. Il nous vint alors à l'esprit en considérant que les racines sont en nombre infini de les rassembler sous un terme unique qui nous servirait à nommer toutes les racines."
Socrates: "et ce terme, l'avez vous trouvé ? "
Thééthète : "je le crois: juges en toi-même ...
Nous avons divisé tous les nombres en deux classes: les uns, les nombres qui peuvent être formés par la multiplication de facteurs égaux, nous les avons représentés sous la figure du carré et nous les avons appelés carrés et équilatères ...
Pour les nombres placés entre les premiers, comme le trois, le cinq et tous les nombres qui ne peuvent être formés en multipliant des facteurs égaux, mais seulement en multipliant un plus grand par un plus petit ou un plus petit par un plus grand et qui s'expriment toujours par une figure aux cotés inégaux, nous les avons représentés sous la figure du rectangle et nous les avons nommés rectangulaires ...
Toutes les lignes dont le carré forme un nombre plan équilatère, nous les avons définies longueurs, et toutes celles dont le carré forme un nombre aux facteurs inégaux, nous les avons définies racines, parce qu'elles ne sont point commensurables avec les autres pour la longueur, mais seulement pour les aires qu'elles ont le pouvoir de former. Et nous avons opéré de même pour les solides."

Point de vue numérique

On peut considérer que ce texte marque le passage d'un point de vue purement géométrique, à un point de vue numérique, au moins partiellement. Ceci est une façon pour Platon de présenter Thééthète comme celui qui a fait progresser la théorie des nombres. Le dialogue de Platon, Le Théétète montre que Théodore , avait prouvé l'irrationalité des lignes que nous désignons par√3, √5, ...,√17,

mais qu'il s'était arrêté là. Son élève, le jeune Théétète mis en scène par Platon "annonce ses découvertes futures", en montrant l'existence d'une infinité d'irrationnelles et en indiquant les moyens de les classer. La mise en scène de Platon montre que Théodore avait démontré rigoureusement l'irrationalité d'un certain nombre de lignes, sans doute par des méthodes géométriques, mais qu'il a rencontré une difficulté au niveau de √17.

Débats d'historiens

Ce texte a suscité beaucoup de recherches en histoire des mathématiques pour trouver l'explication du dix sept. En gros, il y a deux modes d'explications ; l'une est la construction de ce qui est appelé l'escargot de Pythagore constitué de triangles rectangles de coté 1 et √2, ..., √17, car la figure boucle à cette étape. La deuxième mode d'explication est de voir jusqu'où la démonstration par le pair et l'impair est praticable.
C'est à partir de ces dialogues et des Éléments d'Euclide que les historiens des sciences essaient de reconstituer le cheminement des découvertes sur les irrationnelles. Théétète est crédité de démonstrations générales de type arithmétique sur les irrationnelles et de leur classement tel qu'il figure dans le livre 10 des Éléments. D'après le texte même du dialogue, les historiens supposent que Théodore avait établi une démonstration valide pour chacun des cas désignés par Théétète. Que ces démonstrations pouvaient s'appliquer à une infinité d'autres cas et qu'elles utilisaient des constructions géométriques. Ils supposent aussi que les méthodes arithmétiques mises au point par Théétète n'étaient pas disponibles pour Théodore.

La démonstration par le pair et l'impair

Des historiens comme Knorr ont essayé de reconstituer les démonstrations de Théodore en utilisant des arguments connus des pythagoriciens. Tout d'abord, il est facile de voir que la démonstration utilisée pour √2 vaut pour les entiers pairs qui ne sont pas des carrés, à savoir 6, 8, 10, 12, 14. Il reste à s'occuper de 3, 5, 7, 11, 13, 15, 17. Nous allons grouper ces entiers en plusieurs familles.
Remarquons d'abord que si on a A² = N B², avec A et B non tous deux pairs, N étant impair, cela oblige que A et B soient impairs.

A = 2 a + 1 et B = 2 b + 1. Alors A² = NB² se traduit par:

4 a(a + 1)+ 1 = N [4 b(b + 1)+ 1]

N = 4 n + 3: Ceci recouvre les cas des entiers 7, 11, 15. L'égalité précédente se réécrit:
4 n[4 b(b + 1)+ 1] + 12 b(b + 1) + 3 = 4 a(a + 1) + 1

8 n b(b + 1) + 2 n + 6 b(b + 1) + 1 = 2 a(a + 1)
Un nombre pair est égal à un nombre impair: impossible.
N = 8 n + 5: Ceci recouvre les cas des entiers 5 et 13. Si on réécrit la même égalité, on obtient:
8 n + 8 n b(b + 1) + 20 b(b + 1) + 5 = 4 a(a + 1) + 1

2 n + 2 n b(b + 1) + 5 b(b + 1) + 1 = a(a + 1)
Un nombre pair égal à un nombre impair, ce qui est impossible.
8 n + 1: Ceci recouvre le cas 17.
17[4 b(b + 1) + 1] = 4 a(a + 1) + 1

17 b(b + 1) + 4 = a(a + 1)
Égalité de deux nombres pairs qui ne permet pas de conclure.

Justification actuelle

Bien sûr, les démonstrations actuelles utilisent la décomposition en facteurs premiers. Un nombre est le carré d'un entier si et seulement si tous les exposants des facteurs premiers qui figurent dans sa décomposition sont pairs. Tout nombre entier dont un des exposants des facteurs premiers qui figurent dans sa décomposition est impair est un nombre irrationnel. La démonstration de ce fait utilise le théorème de Gauss.

Soit p un facteur d'exposant a impair dans la décomposition de N. Si on suppose une fraction irréductible A/B égale à √ N, A² = N b², on montre que p^a divise A², et donc p^a+1 aussi. L'égalité se simplifie par p^a et permet de montrer ensuite que p divise B et d'obtenir une contradiction.

La méthode d'antiphérèse.

On connaît une autre démonstration de l'incommensurabilité de la diagonale avec le côté du carré que celle par le pair et l'impair évoquée par Aristote. Elle repose sur la méthode d'antiphérèse (ou méthode de soustraction réciproque). On appelle ainsi l'algorithme de recherche d'une commune mesure entre deux lignes décrit dans le livre 10 des Éléments d'Euclide.

Soit un carré ABCD. On reporte sur la diagonale AC une longueur AE égale au côté AB et on mène la perpendiculaire à la diagonale en E qui coupe le côté BC en F. Il est facile de montrer que les triangles rectangles ABF et AEF qui ont leurs diagonales confondues et un côté AB égal au côté AE, sont égaux. Donc BF=EF. Le triangle EFC est un triangle rectangle qui a un angle de 45 degrés donc il est isocèle et EF=EC.

Appliquons maintenant l'algorithme de recherche d'une commune mesure. Une mesure commune à AC et AB est une commune mesure à AB et EC donc à AB et BF. Si on construit le carré EFGC, on est ramené à la recherche d'une commune mesure entre la diagonale FC et le côté EC. On recommence et on obtient un nouveau carré semblable au précédent. Cela montre que le processus ne se termine pas. Il n'y a donc pas de commune mesure.

Calcul de racines carrées

Un algorithme, qui est le plus efficace dans un sens que nous allons préciser ensuite, est obtenu à partir d'idées en apparence très différentes. C'est celui qui est programmé dans les calculettes et qu'on appelle suivant les livres algorithme de Babylone ou algorithme de Héron.

Algorithme de Babylone

On trouve sur une tablette (YBC 7289), le dessin d'un carré et de ses diagonales. Une longueur en sexagésimal est indiquée pour le coté et pour la diagonale. Sous la diagonale est indiqué un nombre sexagésimal 1, 24, 51, 10 qui évalué dans un système décimal fournit la valeur 1,414213 qui est une valeur approchée de √2 à 10^-6 près.

Comment cette valeur a-t-elle pu être trouvée ? On peut seulement, en l'absence de textes écrits, supposer le raisonnement suivant, valable d'ailleurs pour √A, A étant n'importe quel entier non carré.

Si a est une valeur approchée de cette racine, il est facile par un simple calcul d'encadrement constater que a et A/a sont deux valeurs qui encadrent la racine. En prenant la moyenne des deux valeurs, on a des chances d'améliorer la précision, remarque qui a pu être vérifiée empiriquement en élevant le nouveau nombre au carré.

Cela donne en terme de suite :

x_n=

(x_n-1 +

x_n-1

)

Algorithme de Héron

Cette même méthode est exposée dans le texte suivant de Héron. Rappelons la formule de Héron qui permet d'obtenir l'aire S d'un triangle de cotés a, b, c et de périmètre p par la formule:

La méthode exposée ci-après n'est pas la seule méthode employée par Héron. Nous y reviendrons plus tard. Voici l'exposé par Héron d'une méthode de calcul de √720

"Puisque 720 n'a pas de coté rationnel, nous extrairons le coté avec une très petite différence de la façon suivante. Comme le premier nombre carré plus grand que 720 est 729 qui a pour coté 27, divise 720 par 27, cela fait 26 et 2/3 ; ajoute 27, cela fait 532/3 ; prends-en la moitié : cela fait 26 5/6
En fait 26 5/6 multiplié par lui-même donne 720 1/36 ; de sorte que la différence est 1/36.
Si nous voulons rendre cette différence inférieure encore à 1/36, nous mettrons 720 1/36 trouvé tout à l'heure à la place de 729*, et en procédant de la même façon, nous trouverons que la différence est beaucoup plus petite que 1/36."
Les Métriques, livre 1 traduction de Mathématiques au fil des âges.

Algorithme de Descartes ou d'Euler

On peut aboutir au même algorithme à partir du point de vue suivant bien exprimé par Euler (extrait des Éléments d'Algèbre, ch. 785 et 786).

Le premier moyen dont nous parlerons suppose qu'on ait déjà déterminé assez exactement la valeur d'une racine ; qu'on sache, par exemple, qu'une telle valeur surpasse 4 et qu'elle est plus petite que 5. Dans ce cas, si l'on suppose cette valeur 4 + p, on est sûr que p exprime une fraction. Or si p est une fraction, et par conséquent moindre que l'unité, le carré de p, son cube, et en général toutes les puissances plus hautes de p, seront encore beaucoup plus petites que l'unité, et cela fait que, puisqu'il s'agit d'une approximation, on peut les omettre dans le calcul.

Partant d'une valeur approchée a de √A, nous cherchons à l'améliorer en introduisant un terme correcteur h. On cherche (a + h)² = A = a² + 2 a h + h². Négligeons h². On prend h = (A - a²)/2 a. Alors la nouvelle valeur approchée est h = (A + a²)/2 a = 1/2(a + A/a)

Algorithme de Newton

On retrouve encore cet algorithme sous la forme de l'algorithme de Newton, qui expose sa méthode en 1669 sans donner d'interprétation géométrique ; celle-ci est l'oeuvre de Raphson puis la justification celle de Fourier. On considère la courbe y = x² - A et on cherche la valeur de x pour laquelle y = 0. Partant d'une valeur proche a de la racine, on trace la tangente à la courbe au point (a, a² - A). La tangente à la courbe a pour équation

y - (a² - A) = 2 a(x - a)

Alors on obtient pour l'intersection de cette tangente avec l'axe des x la valeur x = A + a²/2 a, ce qui est la valeur donnée par les autres méthodes.

Justification de la convergence

Convergence de cet algorithme

Voici l'étude la convergence de cet algorithme dans le cas de √2 sous forme de problème.
Dans le plan xoy, on porte sur ox une suite de points a₁, ..., a_n... et sur Oy une suite de points b₁, ..., b_n,..., construites de la façon suivante :

1) a₁ = 2 et b₁ = 1

2) a_n = (a_n-1+ b_n-1)/2

3) a_nb_n = 2

Représenter cette suite de rectangles de cotés a_n et b_n.

Démontrer les trois propriétés suivantes : " n, b_n < a_n, la suite (a_n)_{n Î N} est décroissante, la suite (b_n)_{n Î N} est croissante.

Calculer a_n - b_n en fonction de a_n-1 - b_n-1 et de a_n. Montrer que l'on a l'inégalité :

a_n - b_n <

(a_n-1 - b_n-1)²

Calculer les premiers termes de la suite (a_n)_{n Î N}. Combien de décimales exactes a -t-on à chaque fois ? Utiliser l'inégalité précédente pour montrer que le nombre de décimales exactes double à chaque fois.

Autre justification de la convergence

On peut aussi justifier la convergence de l'algorithme par les théorèmes sur les suites récurrentes. On trace le graphe de la fonction

f(x) =

(x +

)

et on justifie la convergence vers le point fixe solution de x = f(x)

Calcul par les fractions continues

Le procédé grec d'antiphérèse a fourni aux Grecs le moyens de trouver un algorithme d'approximation de√2 de la façon suivante.

On pose FC = d, EC = s, alors si on évalue le côté du carré ABCD et sa diagonale en fonction de d et de s, on obtient AB = d + s et AC = d + 2s. Définissons une double suite :

d_n+1 = d_n + 2 s_n, s_n+1 = d_n + s_n.

On obtient facilement que

d_n+1² - 2 s_n+1² = 2 s_n² - d_n².

Il suffit alors de se donner pour point de départ des deux suites s₀ = 1 et d₀ = 1 pour obtenir +1 ou -1 pour la quantité d_n² - 2s_n². La suite des rapports d_n /s_n converge vers √2. Les premières valeurs sont 3 /2, 7 /5 utilisé par Aristaque, 17 /12 utilisé par Héron.

Cet algorithme revient, avec les notations qui sont les nôtres, à faire un développement en fraction continue. Si nous écrivons de cette façon le développement de √2, nous obtenons :

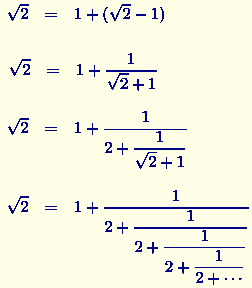
$fracracine2$

On peut aussi noter √2 = á1,2,2,2,2, ...ñ.

On peut constater que cet algorithme fournit les mêmes approximations que l'algorithme du coté et de la diagonale. Si p_n/q_n est une approximation, la valeur suivante se calcule comme :

$frac$

Les fractions continues ont joué un rôle fondamental dans l'histoire des approximations.

Approximations décimales

Les travaux d'approximation de rapports par des rationnels et amènent les mathématiciens à s'interroger sur le statut des rapports irrationnels. Sont-ce des nombres ou sont-ils associées à des nombres ?

Les décimaux

La découverte des décimaux chez les arabes et leur redécouverte en Europe poussent certains mathématiciens à des prises de position nettes sur cette question. Le contexte dans lequel est apparue la théorie des décimaux est important, lié à la fois à des calculs sur les polynômes, et à des calculs d'extractions de racines n^e. Les traces de la diffusion de ce savoir vers l'Europe sont très parcellaires, mais attestées. Les décimaux semblent avoir fait l'objet d'une redécouverte en Europe au seizième siècle, par plusieurs auteurs dont le plus connu est Stévin. Les décimaux ont tout de suite été utilisés, par exemple par Viète pour la détermination d'approximations sous forme de fractions décimales des solutions positives d'équations algébriques, et pour l'établissement des tables de logarithmes. L'extension formelle des décimaux aux développements décimaux illimités attendra le développement de l'analyse (en 1742 dans un texte de John Marsch). Plus tard, certains voudront les utiliser pour considérer les irrationnels comme des nombres définis par un développement décimal illimité. Cependant leur usage posera les questions suivantes : le développement décimal illimité des fractions est périodique ; il y a une loi pour écrire les chiffres ; le développement décimal illimité des irrationnels n'a pas de loi ; n'est ce pas un objet vide ?

Décimaux et calcul de racines carrées

Pour le calcul de racines carrées, on a déjà vu un algorithme, sous le nom d'algorithme de Babylone et d'algorithme de Héron, où le nombre de chiffres décimaux exacts double à chaque pas d'itération. Voyons maintenant un algorithme qui détermine les chiffres décimaux successifs d'une racine carrée.

Newton a beaucoup travaillé sur les calculs d'approximations de racines d'ordre quelconque, à l'aide de décimaux. Voici un exemple de calcul d'une racine carrée par Newton,(Lectures on algebra p. 88.). Ce texte décrit une méthode qui a été enseignée en France jusqu'au développement des calculettes.

Il s'agit d'extraire la racine carrée de 99856. Cet algorithme détermine successivement les chiffres en partant de ceux d'ordre le plus élevé. Il repose entièrement sur l'identité algébrique (A + b)² = A² + 2 A b + b². On suppose qu'à une étape on ait déjà déterminé A, qu'on ait retiré au nombre donné le carré de A et qu'on cherche le chiffre b suivant ce qui revient à appliquer l'identité avec (A × 10 +b)². Il faut donc retirer 2 × (A × 10) × b + b², ce qui explique que Newton double d'abord le nombre A avant de lui juxtaposer le chiffre b pour retirer (2 × (A × 10) + b) × b et donc avoir retiré le carré du nouveau nombre obtenu à cette nouvelle étape.

La première étape consiste à partager ce nombre en tranches de deux chiffres : 9^.98^.56. On cherche le plus grand nombre dont le carré soit 9. On obtient 3, premier chiffre de la racine cherchée et on retire son carré au premier bloc sur le gauche. Il reste 0. Le nombre cherché commence par un 3.

On abaisse la deuxième tranche 98, on double le premier chiffre 3 obtenu et on cherche le plus grand chiffre b tel que 6b × b soit inférieur à 98. Cela revient à chercher combien de fois 6 est contenu dans 9. On obtient b = 1 comme deuxième chiffre. On retire 61 à 98, on obtient 37. Le nombre cherché commence par 31.

On abaisse la troisième tranche et on travaille maintenant avec 3756. On double le nombre 31 obtenu comme début de notre racine. On obtient 62 et on cherche un troisième chiffre c tel que 62c × c soit le plus grand possible inférieur à 3756, ce qui revient à diviser 375 par 62. On obtient c=6. On retire à 3756 le nombre 626 × 6 = 3756, on obtient 0. Le nombre de départ est un carré 99856= 316².

Pour extraire la racine carrée d'un entier qui n'est pas un carré, ou d'un nombre décimal la même méthode s'applique en partageant le nombre en tranches de deux chiffres de part et d'autre du point décimal. La suite du texte traite les extractions de racines cubiques etc.

Bibliographie : Les nombres irrationnels

Barbin: Saisir l'irrationnel : Dire, montrer, faire toucher, tenir, APMEP numéro 400 septembre 1995.
Cousquer: La fabuleuse histoire des nombres édition Diderot, 1998.
Daumas: Activités en classe sur l'irrationalité de Pythagore à Théon de Smyrne, Contribution à une approche historique de l'enseignement des mathématiques Besançon 1995.
Daumas: Une approche de l'irrationalité : algorithme d'Euclide et fractions continues Commission Inter Irem épistémologie et histoire des mathématiques, Histoire d'infini Landerneau 1992.
Houzel: Qu'est-ce qu'un nombre réel ? La Recherche Novembre 1995.
IREM: Histoires de problèmes, histoire des mathématiques, Faut-il toujours raison garder et En route vers l'infini Ellipses, 1993.
Jaboeuf: Les fractions continues, revue Quadrature numéros 1 à 6.
Thomas, Van Dieren, Rouche: Mesures, pavages et nombres irrationnels, GEM Louvain la Neuve.

Partager cet article

Repost0

Published by Eliane Cousquer - dans histoire des mathématiques
commenter cet article …